I love reading science fiction. I know, shocker, right? The geek who loves sci-fi. My obsession with sci-fi goes back as long as I can remember and has been a source of enormous joy and has certainly stimulated my imagination and influenced my scientific tinkering. One of the earliest novels I remember reading was The Time of the Great Freeze by Robert Silverberg.
The story is set 600 years in the future when the earth has been ensconced in a sheet of ice, virtually from pole to pole. People live huddled in underground cities, preferring authoritarian rule to being cast out in the sub-zero wasteland that lies above. This story really captured my childhood imagination and although the book is not well regarded in the sci-fi world, it really had an impact on me. It’s interesting to note that the book was first published in the 1960’s and reflects the then scientific consensus that the world was heading towards another ice age. This notion held sway through all of the 1970’s and on into the 1980’s. Then, seemingly overnight, the perspective changed, no ice age for us! Pull out the water wings. Hmm.
I’ve always enjoyed stories about cultures lost, of Forerunner species who spread far and wide through the cosmos, building civilizations of staggering complexity…only to wither and succumb to the onslaught of time. Andre Norton was my favorite childhood author in this genre, while Jack Mcdevitt has written a number of phenomenal books in this theme. I’m not sure why, but it’s so fascinating thinking about these far away cultures that reached amazing levels of sophistication…and then simply ceased to exist. Why? The authors rarely offer specific details, that’s part of the mystery, but it makes for good reading and even better pondering.
Now, this line of reasoning…that cultures grow, evolve and then die will likely strike many folks as “wrong” or counter intuitive. That there have been a number of highly advanced civilizations that have come and gone over the past 10,000 years or so is unfortunately, a shock (shrug?) for most people. Few realize the remarkable sophistication of the pre-Columbian, Central and South American civilizations, nor do people realize that the ancient Greek & Roman civilizations had most of the trappings necessary to enter the Industrial Revolution, which would not occur for nearly a thousand years after Rome’s collapse.
When in Rome
I’m by no means a historian, but I am a fan of certain time periods other than the Paleolithic. One of my favorite areas of study is the dissolution of the Roman civilization and the rise of the Dark Ages (I know most modern historians dislike the term “dark ages”…like I said, I’m NOT a historian!). The technology and knowledge base of the ancients is nothing short of amazing. Take the ancient Greek Antikythera mechanism. This contraption was built over 2,000 years ago and appears to have been a complex analog computer that could precisely calculate the positions of celestial bodies. The level of craftsmanship necessary to produce the gears was not seen again until the 19th century. It’s fairly reasonable to assume this was in fact not the first machine of its kind and that precursors were likely in development for several hundred years, which pushes the technology back even further. Then we have the Roman Aeolipile, a steam engine precursor which predated the Industrial Revolution by nearly 2,000 years. Now, this topic has actually been the subject of some very good alternate history sci-fi. “What if” the Roman Empire had NOT collapsed? They were just starting to exploit coal reserves instead of wood and water, they had advanced mathematics, the ability to use mechanical calculation tools and although iron was not yet on their list of technologies, that would obviously just be a matter of time. Some speculate that if Rome had not collapsed we’d be terra-forming Mars right now. Or the Earth would be a crispy radioactive cinder. Interesting stories either way. What is crystal clear however is these early civilizations reached far across the globe, had enormous influence, possessed remarkable levels of technology and culture…and eventually collapsed and were consumed by time. It took almost 2,000 years to reach similar levels of civilization and technology. Unlike the sci-fi novels which leave the demise of Forerunner species largely to the imagination of the reader, we know why civilizations tend collapse:
1-Getting over extended militarily
2-Producing a large and ever growing entitlement class
3-Falling prey to professional politicians who keep the wheels spinning on the above two issues until the wheels fall off the whole damn system.
For the folks who get your panties bunched about my Libertarian leanings, don’t worry, this is not politics, just history :0P
So, you may be asking yourself “What the hell does this history survey have to do with nutrition, medicine and health?” Well, quite a bit when we consider the following story. A lone doctor put the pieces of the leaky gut/autoimmunity story together almost 50 years ago. He saw the connections between intestinal permeability and diseases such as rheumatoid arthritis and multiple sclerosis. He published his findings, he helped the people in his care…and his amazing insights eventually died, were buried and nearly lost to time. Loren Cordain shot me the following two papers from Dr. R. Shatin:
When I read those papers, particularly the first one, all I could do was think “WOW!!”
Dr. Shatin had pieced together the connection between gut permeability, celiac disease rheumatoid arthritis and multiple sclerosis.
In the early 1960’s.
He also had a clear grasp of the influence of evolution in health and disease. I’d wager it was using the evolutionary template that lead to his subsequent observations regarding intestinal permeability and autoimmunity, but we have precious little information about Dr. Shatin. Dr. Ben Balzer did some digging and at present this is what we have:
Dear Dr Balzer
Thanks for your email enquiry of 13 April 2012 seeking information about Dr R Shatin a prominent doctor from The Alfred hospital who published some significant papers regarding diet and disease in the 1960’s which are of continuing interest to doctors and scientists who study the Paleolithic Diet and its relevance to modern health. It is pleasing to note your observation that Dr Shatin’s studies are prescient indicating he is one of the many leading doctors and nurses who have made The Alfred a world class treating and teaching hospital.
I have checked The Alfred hospital’s archives and found that Roman Shatin graduated as M. B. B. S. (Melb.) in 1935 and worked at The Alfred from 1947 to his retirement on 1 July 1977. His main role was Medical Clinical Assistant (1947 – 1955), Senior Medical Clinical Assistant (1956 – 1976) and Honorary Clinical Assistant (1976-77).
I am aware of one of Dr R Shatin‘s publications namely Man and His Cultigens – R Shatin (Scientific Australian March 1964).
I regret not having more information on Dr R Shatin and would appreciate your forwarding me any more information you come across. Although there have been a number of publications covering The Alfred’s history (The Hospital South of the Yarra, A history of Alfred Hospital Melbourne from foundation to the nineteen-forties, Ann M Mitchell, the Griffin Press SA 1977 and Alfred Hospital Faces and Places Volume I, II, III & IV Published by The Alfred Heritage Committee between 1996 and 2010), I am surprised there is no mention of Dr Shatin who served the hospital for 30 years.
Thanks again for this enquiry.
Peter Frawley
Archivist
The Alfred Hospital & Caulfield Hospital
16 April 2012
You folks in Australia should be damn proud. One of the biggest thinkers in the Paleo/Ancestral health scene is one of your own, and he was fighting the good fight a half century ago.
I want to look at some specific observations from the two papers and talk a little about how significant and prescient that material is/was. Let’s look at the first paper first starting with an observation about the field of autoimmunity:
In the field of rheumatic disorders the currently prevailing theory of autoimmunity has failed to establish causes or promote cures. An alternative concept has been advanced by the present author (1963)6. This concept is based on the postulate of man’s maladaptation to biologically new food. Evidence for the presence of this maladaptaton; considered in this concept to be the genetic (inherited) susceptibility to rheumatic diseases, is based on: (a) clinical observation; (b) a pilot trial of treatment, 19646; and (c) recent advances in biochemistry, genetics and gastroenterology including the study of the small intestine on the one hand and clues from paleopathology on the other.
It’s interesting, one must look very hard at the current models to see the connection between intestinal permeability and autoimmunity. Hygiene hypothesis is about as close to it gets. But one does not ever see commentary about evolutionary/genetic discord. That Dr. Shatin connected these dots so long ago is remarkable. Then this:
Briefly, in the concept advanced here, it is suggested that the cereals wheat and rye, the biologically new food (hitherto probably only avian food), were not universally suited to human metabolism because of their protein component, gluten.
Celiac disease had only reached prominence in the medical community a few decades earlier. That Dr. Shatin was able to piece all this together is remarkable. I’ll leave you to peruse those two papers, but I think it’s worth asking: Why did this information almost disappear from history? Dr. Shatin performed clinical trials showing a paleo diet to be beneficial for RA. He knew a remarkable amount of what we know today with regards to intestinal permeability and autoimmunity, but like the Aeolipile this technology and understanding has largely been lost to a Dark Age of reductionist medicine. I think it’s pretty clear what happened here: This man’s ideas were counter to the CONSENSUS (I have a piece brewing on scientific consensus) and so the ideas were ignored, likely ridiculed (nearly) out of existence. The changes that are afoot today are NOT happening from consensus and are certainly not coming from the scientific and academic mainstream. Yet. The change we are benefiting from today is happening because with social networks we can effectively step outside the “consensus” and do things that actually “work.” We are seeing N=1 experiments with the Paleo/Ancestral Health template performed millions of times per day. If it did not work, if this way of doing things did not benefit autoimmunity and a host of other issues, the concept would wither and die. It appears to be doing anything but that.
Don’t get too smug though, any good sci-fi novel will remind you that decay and entropy are the norm, not the exception. So too apparently are totalitarian power grabs, especially when the dominant paradigm is being eroded. Case in point:
The North Carolina Board of Dietetics and Nutrition (NCBDN) is threatening to sue, shut down and SEND TO JAIL a type1 diabetic man who has found a way out of the system of managed death. It’s worth noting that the ADA reviewers do NOT see recommending a vegetarian diet as being problematic…
The NCBDN will apparently forcibly confine and silence those people who do not stay within certain “Party” guidelines. This on the heels of the Forbes piece implicating the ADA for forming what is essentially a monopoly on nutrition advice. Which created some seriously bunched britches on the part of the ADA. I find it hilarious that I need to sit through a Sugar Free Coffee Mate ad on the Food Management site before being allowed to proceed to the response. THESE people are in charge of our food policy?
That the Internet and social media have allowed the concept of Ancestral Health to be broadcast to the masses is undeniable. It is also not surprising that we are witnessing an attempt by the government and academic institutions to silence our attempts at self determination. If we are not sick, fat and dying from the subsidized foods the government and ADA wants to feed us, what NEED is there for the ADA?
I don’t know about you, but I will not allow another Dark Ages to hamstring medicine and be set back 50 years. Again.
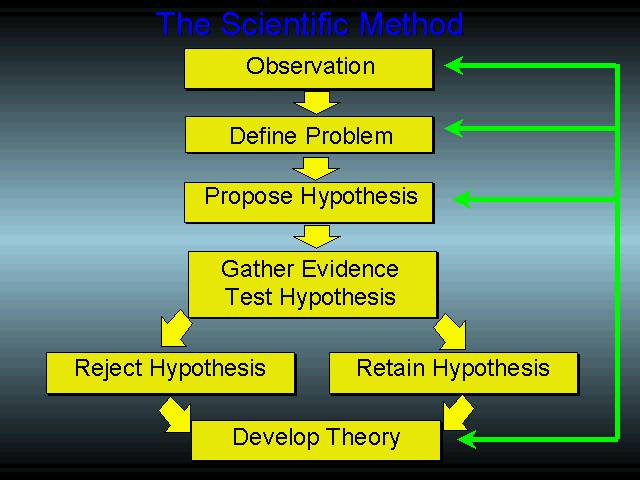
The ADA has a serious problem if it chooses to try to wrest control of our ability to TALK about food and it can be proven in court. They do not practice their craft from a legitimate scientific position. Don’t worry my New Earth Creationist pals, I’m not even talking about the fact the ADA is not on a firm epistemological footing with regards to Evolution, what I’m talking about is the scientific method MUST follow this process:
“Nutritional science” largely stops at hypothesis generation, yet they are allowed to dictate public nutrition policy. They use epidemiological studies to try to support their case, but this is correlation, not causation. When it comes down to actual, randomized controlled trials we consistently see low-carb interventions trumping the grain centric recommendations of the government. The ADA is not practicing science, this can be proven in a court of law and it could eviscerate the Clergy masquerading as scientists.
Now as much as I might like a good fight (and we may need to roll up a newspaper and paddle the ADA’s backside a bit legally) there is likely a better way to win this battle. Instead of fighting a legal (or even ideological) war with the leaders of these organisations, why not change the culture from the bottom, with the people who will be the leaders tomorrow? Maybe we start offering scholarships for undergrad and graduate nutrition majors who choose to conduct research in the Ancestral Health/Paleo/evolutionary biology realm? Best essays and research proposals win the cash. For the cost of one hard fought court battle we could have scholarships in EVERY nutritional science program in the world.
Markets, incentives and innovation might just win the day. Shocker.
It’s interesting, when I started writing this piece my only intent was to pay homage to a great physician and scientist who saw remarkable connections between ecology and health over 50 years ago. In the midst of this process the Reason Magazine piece was released and it gave me significant pause. As far as we’ve come, as much as we’ve gained…it could all go away. SOPA was a terrifying prospect, which we managed to put down. This time. Now this.
I can assure you most of the folks living at the end of the Roman era did not see the problems surrounding them. They had indoor plumbing, heated floors, arts, entertainment…what could possibly go wrong?



Robb, once again you are on to something big and life changing. Yes, we can do better, our community can effect change, and we can fight the good fight from the bottom up. No war, no military, no out in the public fights between Paleo and Vegan camps – just a healthy force of people bubbling up and growing in numbers simply by doing what we know to be natural, healthy and right. It’s our own real-time sci fi adventure. Take the lead Robb, sally forth and we’ll follow behind you.
Great Blog Robb.
The core of the problem is that society does not value science as much as it should. It’s far too easy and acceptable for people to pass on non answers to important questions. The number of times I’ve heard smart individuals fall back on “everything in moderation” when discussing nutrition is disturbing.
As you’ve stated, the advent of social media and the internet has connected us like never before. Good information and bad is now identified as such much quicker and bullshit is debunked at an exponential rate. However, when it comes to nutrition a tiny (but growing) body of good info is swamped in a sea of bad so it’s imperative that people like yourself use your soapboxes to good effect.
Keep up the good work.
Cheers,
Clyde
“The core of the problem is that society does not value science as much as it should.”
I’d guess what seems to be a history of “science” so frequently reaching erroneous conclusions on major topics goes a long way to explaining why that is the case.
I think the media is kinda complicit in this, but a good point.
Perhaps the only hope is to spread the idea of Paleo eating enough that it will be impossible to suppress in the future.
That seems to be the plan.
I just want to say that since day one, when we started learning all about Paleo I chose your book over all the others and I was glad I did. I have been following Lee Saxby and the practice of barefoot running and came across your book and what makes it, is your writing style which is so engaging and free of B.S which is a palpable personality from beginning to end in all you do.
Kudos to you!
Thanks Angel! Made my day.
You’re a true leader Robb! Quickly becoming the Marcus Aurelius or our time with posts like these…keep them coming. The younger generation is here and ready to learn and create ground up change.
I’m guessing you’ve read it (but maybe not) anyways… I bet you’ll dig this book written in 1951 on successful diet interventions for Celiac Disease. http://www.amazon.com/Management-Celiac-Disease-Sidney-Valentine/dp/1258196212
Thanks Steven and no, I’ve no read that. I’m on it!
He goes back farther than 1951, FYI from Wikipedia re Haas: http://goo.gl/UMgx9
“In a 1924 study, Haas reported, “In cases which the diet can be controlled for a sufficient long time, recovery ensues in every instance and without nutritional relapse.”[2]
In 1922, Kleinschmidt wrote a scientific paper about the efficacy of Dr Haas’s diet, stating, “The prognosis in celiac disease has undergone a complete change during the last few years. The discouraging results of the previous methods of treatment have entirely disappeared since we have followed the diet of the American, Haas.”[3] In 1928, Von den Steinen reported on a study which validated the efficacy of Dr Haas’ diet and verified its results.[4] Haas also wrote a 1955 case report on 191 patients treated with the diet.[5]”
Amen!! Bottom Up Grass Roots that’s how it works!! I teach my kids to fight the “My Plate” education they get at school and they teach their kids and maybe someday we will be out of the grips of failed systems like ADA & USDA!!
Rob,
Wow! This is HUGE news! Great find! I was just commenting to someone about the NCBDN vs. blogger case that this isn’t one bit about him not being licensed and every bit about the establishment trying to gag those who speaking out against the establishment. I speculate that were he to have been a licensed dietician/nutritionist/whatever, they’d simply be seeking to revoke said license. The fact that he’s unlicensed is merely a convenient legal avenue for them to pursue shutting him down.
And when you think about the whole concept of licensing professions in the first place, it’s really to make sure that everyone tows the same line; from plumbers to doctors to driving, everyone needs to do things exactly the same way. In some cases this makes sense and is even beneficial. However, it also leads to a blindness of innovation and improvement. And in this case, what we’re seeing isn’t really that much different than the recording industry sue over digital sharing. The established power base is merely attempting to protect their profit center. That’s all that’s going on here!
The good news is, we’ve got a growing grass-roots movement continually calling BS on them every step of the way. There’s a war brewing, and in the end, even this beast will fall to our millions of atlatls 🙂
Great post, Robb. I am really interested in one of the references you have highlighted at the end of the 1964 article (Role of Food Allergy in Multiple Sclerosis), but I can’t quite make out the cited information. Is this from a publication called Neurology? And is it available somewhere? My mom and her sister have MS and I’m always on top of the MS stuff. Would LOVE to read the article.
It’s interesting, I came to the Paleo world in a round-about way, by researching how to protect myself from MS. I was very intrigued by Dr. Ashton Embry’s research into diet and Vitamin D with regards to MS. His son’s MS has been in complete remission, thanks to Dr. Embry’s research.
The two papers you posted reminded me of a paper Dr. Ashton Embry has on his website http://www.direct-ms.org. It was written by Roger MacDougall who was healing himself from MS at about the same time as the articles you posted were written. He cured himself of MS by adopting a Paleolithic diet and published a pamphlet detailing his diet in the 80’s.
Reading things like this just make me so angry. My mother was diagnosed with MS when she was 36. 36!! (Her sister was also diagnosed in her 30s, but has since passed away). And not a single physician that she has seen over the past 24 years has offered her anything but physical therapy and injections that kill her immune system (and not surprisingly cost several hundred $$ a month.) How can information like this die?!?!?!? How can so many people heal themselves and physicians do not take notice? It’s tantamount to malpractice! How LONG do people like Terry Wahls (a living, breathing specimen) have to walk around and shout at the top of their lungs about nutritional healing before the “establishment” will take notice?
I am 39 years old and my health started falling apart when I was 35. 35! I may have been one year away from my mother’s diagnosis had I not taken my health into my own hands, spent hours, and days and months researching and pushing back against EVERY physician that I went to, INSISTING that we find the CAUSE of my issues and not just treating the symptoms. It took me three years to find a physician who would listen to me and was not put off by the fact that I wanted to be in charge of my health. Together we discovered that I had Celiac Disease and dairy allergy. I corrected my diet and today I am healthy as an ox. But in order to get here, I had to fight the medical establishment tooth and nail and that’s just WRONG. If I had taken all the “treatment” I was offered, I would be taking PPIs, anti-depressants, anti-anxiety meds, sleeping pills and rubbing cream on my face for rosacea and would very likely be suffering my mom’s fate.
I’m pissed. REALLY pissed. And I get more so every goddam day. People are missing out on HEALING because the “authorities” have their heads in their asses and have been taught to see what they believe instead of believing what they see. And I’m not all that inclined to believe that it will change anytime soon. The current treatment for MS is a cash cow (weekly injections at a few hundred dollars a pop). There is no money in allowing people to heal themselves with diet. We are battling money…BIG MONEY…INCONCEIVABLE AMOUNTS OF MONEY…plain and simple.
Ok, I’ve gotta stop ranting or I’m not going to be able to sleep. I’m going to go chug my fizzy magnesium and meditate and let someone else worry about the fate of the world. But seriously, if you have any information on where I can get my hands on that article, I would be much obliged.
muchas gracias,
shannah
Shanna-
Not sure on the reference either, I’ll see if I can get originals on these and post better copies.
I think I mentioned this recently, but Nicki’s mom died from RA complications about 3 months before I met Nicki. Talk about anger. And this is part of why I generally tell the folks who are advocating for the licensure to mean something to GFY. The RD/MD get’s it wrong, people die and from things besides “high protein damaging the kidneys…”
Robb,
I enjoyed your blog post very much but found a few things “off”. I don’t believe Steve, the Diabetic Warrior, is a type 1 diabetic (autoimmune, incurable) but a former type 2 diabetic, which may be reversed with diet. I’m not here to say paleo is the best diet or that a vegetarian plan to fight diabetes is the way to go either. I do take issue with people practicing medicine without a medical license and charging for it. Unfortunately that is what Steve was/is doing. He’d be better off writing another Paleo diet book with a disclaimer “I’m not a medical professional” but here’s my success story and what I did to change my life.
No question about it, diabetes is a dangerous disease and needs to be monitored by a team of specialists, a nutritionist/RD may be a part of that team. There are a number of certified diabetic practitioners who understand a low carb diet may be beneficial for certain individuals, but there may be others who may be harmed by such a heavy protein/nitrogen load on the kidneys and liver. How would Steve diagnosis these individuals? Does he know he could also be sued for giving the wrong dietary advice? There are other co-morbidity problems that go hand in hand with diabetes.
Freedom of speech is one thing, practicing medicine without a license is another.
Deb-
I thought for sure he was Type 1, i’ll double check that and i’ll credit you with the catch on that if I need to change it. You will find this ironic, but I DO agree with you more so than not but here is the rub: MOST RD’s do not understand the benefit of a low carb diet. Nor do they understand that low carb need not be protein intensive (you might be in this category…I’m basing this off your comment, forgive me if I’m wrong). The story here is an automobile mechanic who “gets” the basic ideas of paleo/evolutionary biology may be a greater asset in someones health than ANY Standard of Care RD. Did you read my post on the Paleo Risk Assessment program? Did you read the section where the RD’s in the program have needed to be fired because they refuse to follow the MD PRESCRIBED ketogenic diet? This is pathological!
As an interesting aside: A quick google search found quite a number of vegan “nutrition coaches” in North Carolina. None are RD’s, none appear to be getting hassled http://www.vegancoach.com/vegan-nutrition-coaching.html
I guess the vegan gig is ok, because it’s just full of heart healthy carbs?
What you are saying is we should defer to medical professionals who are driving us the wrong way down the street. My Libertarian self is crying out “bullshit” because if the authorities are wrong, it’s time to take matters into our own hands. Can I sue all the current RD’s for giving the “wrong dietary advice?” I think I both can, and we just might do that.The class action suit looks like this: You are insulin resistant and or a Type 2 diabetic. You have been counseled to eat a 60% carb, grain based diet (standard of care) that is clearly “bad advice” and that RD get’s sued. This is possible because Are the recommendations are not supported by: 1-Evolutionary Theory, 2-Randomized controlled trials.
If the professionals would get their collective act together we would not need free-lancers to simply save our own lives.
Ironic, isn’t it, that the “licensed” medical professionals are all wrong, yet legally protected, and the “unlicensed”, non-medical professional happens to be completely right, backed by science, and yet is being threatened with lawsuits and shutdown?
THAT is a god-damned problem. A big one.
“If the professionals would get their collective act together we would not need free-lancers to simply save our own lives.”
AMEN.
He also has at the bottom of every page that he is NOT a doctor, dietician yada yada yada. It’s his story of healing, and he has a right to broadcast it on his blog. As many of us do ourselves. If someone in NC reads MY blog, does that mean I’m also in violation and should go to jail?
Hi Robb,
Thanks for your reply. Just thought I’d stop by and confirm that yes indeed Steve is a former Type 2 diabetic. If you go to the second page on his “about me” link he states it in an update. Secondly I took a look at the vegan website you included in your reply. Here’s the main difference between Steve’s website and Sassy’s. Sassy doesn’t suggest a “cure” for any kind of disease, which may be why no one is going after her.
True on both counts Debra, thanks.
“I do take issue with people practicing medicine without a medical license and charging for it. Unfortunately that is what Steve was/is doing”
I take issue with people that ignore the fact he does have a disclaimer on his website and makes it perfectly clear he is neither licensed nor a “trained” professional
Great post, btw, Robb.
Rob, thank you for this article. Is there a way we can clone you or your brain?
The world could you several dozen more of you.
HA! My wife would argue strongly agains this.
Awesome post – once again a dose of sanity in an otherwise crazy world. Money may fund the agendas of the ADA and USDA – but money can’t buy health, not true health anyway. Once people start getting that things are gonna change! We’re going to make it happen!! 🙂
Your last paragraph seems to imply that we might be headed to a rather bleak future. Unfortunately, I fear the risk for another “dark ages” is quite high now. I hope the hell I’m wrong. An economic collapse could bring about even more oppressive government. But, reason, logic and science are very powerful tools. Keep up the fight. I know I am…
Much of the world is printing money, the US continues to have a foreign policy that is insane. Shit could get tough for us.
Feel free to move here to Australia should that happen! (I don’t know if you’ve heard of the Gold Coast?)
I would love to show you and your wife and the little Wolf Cub around 😀
…but fingers crossed it doesnt. haha
Rich, rich insights, Robb. (As usual.) You continue to set your own philosophical bar pretty high, y’know. Good thing all the n-3s in the grass-fed beef and other good foods will keep your brain sharp enough to keep topping yourself! 🙂 (As long as you keep getting enough sleep after the cub arrives…)
Anyway, you may have single-handedly reformed my opinion of “social media.” I’m generally not a huge fan of the automation of EVERYTHING, and I do think the constant onslaught of FB/Twitter/what-have-you gives us a sense of connectedness that doesn’t quite match up to real life, face-to-face interactions, looking into someone’s eyes when you speak to them, etc.
That being said, I never really looked at the Internet from the POV you describe below. This new, nonstop interconnectedness that bugs me sometimes is the very thing that makes ideas like ancestral health and low-carb accessible to people who desperately need it and will never hear it from their doctors, dieticians, or the 6 o’clock news. Heaven knows when I was a newbie low carber about 9 years ago, various forums and websites were my only guide, and thank goodness for them. My best teacher is obviously my own body (those n=1 experiments we need and depend on as individuals), but I absolutely cannot overstate how much I learned from *other people’s experiences* that were shared on those forums.
Think of all the parents out there with kids on the spectrum, or people suffering horrific GI issues, or struggling to lose body fat while following the standard “eat less/move more” paradigm, that would never, ever have heard anything about a Paleo or GAPS-type protocol were it not for websites like yours that provide not only the science, but other people’s accounts of healing so remarkable it makes you want to shout about this to as many people as fast as you can.
(When does anecdotal evidence stop being anecdotal, anyway? When a hundred people have great results? A thousand? Ten thousand? I think we’re THERE already. I know all about RCTs, and I know that’s what the community needs going forward if we’re ever gonna change the medical orthodoxy, but I wish people would just take the frakking blinders off and stop *waiting* for the NEJM to publish a study that proves beyond a shadow of a doubt that real food, sunlight, and intelligent movement are good for us.)
What really breaks my heart about some of this leaky gut research from half a century ago is looking back on what they used to do (and still do, to a degree) with those “wacky” family members — the ones with schizophrenia, autism, and all the other ones — they were shoved away in institutions and pretty much discarded by their families and society in general. They were literally “head cases” and separated from the rest of the world, when who knows if healing those guts and getting rid of the grains and other dietary irritants would have had those people functioning well and living optimal lives?
I’m graduating with an MS in nutrition and the talk of the AND (formerly ADA) gaining a legal monopoly on nutrition counseling terrifies me. The people with CNS and CCN credentials are railing against it because it Just. Cannot. Be. Allowed. To. Happen. (The reputation of the AND gives people like Amy Kubal and Stephanie Gruenke a bad name. We tend to lump all RDs in with the Ensure and orange juice folks. Social media is good for dispelling problems like that, too. We all know plenty of MDs who are completely steeped in the [failing] standards of care, but look how many practitioners are starting to come around. Many more NDs,DCs and DOs at the moment, but more and more MDs are seeing the light. Many of them as a result of *their own* struggles to lose weight, treat IBS, etc. – when they learned for themselves that following the advice they’ve given patients for years did NOT work.)
I’m a tad concerned that when the clinical trials of Paleo vs vegan vs SAD or whatever do get underway, they’re going to suffer from the reductionism you mentioned. Obviously, the results will be staggering, but I’m worried the researchers will try to pinpoint the one thing, the magic bullet, that makes Paleo the best option. (Assuming it will be, of course.) They’ll debate whether it’s the reduction in fructose, or the restored n-3/n-6 balance, or the elimination of dairy and grans, when in fact, it’s ALL of that – PLUS the sleep, PLUS the exercise, PLUS the fresh air. I’m holding onto hope that someone involved in those studies will be a big picture thinker like you, Robb.
“The changes that are afoot today are NOT happening from consensus and are certainly not coming from the scientific and academic mainstream. Yet. The change we are benefiting from today is happening because with social networks we can effectively step outside the “consensus” and do things that actually “work.” We are seeing N=1 experiments with the Paleo/Ancestral Health template performed millions of times per day. If it did not work, if this way of doing things did not benefit autoimmunity and a host of other issues, the concept would wither and die. It appears to be doing anything but that.”
Most of the research proposals I’m looking at and involved in are looking bigger picture and outcome. So I think we’ll avoid a little of the reductionist problems.
the social media stuff is AMAZING…I think it’s just knowing when to turn it OFF!
Glad to hear that. I was a little worried that someone’s gonna try to identify the one, specific thing that ancestral diets do that is the single factor in health improvement, and then it would only be a matter of time before they’re trying to make it into a pill or injection. They already have pharmaceutical strength fish oils…oy vey.
But when I stop to think about it, the people even willing to get involved in a trial that looks at an eating paradigm based on evolutionary biology are probably not the reductionist types anyway.
Yea…I mean don’t lose faith in people screwing this up! But I think we’ll be ok. Also, found something you’d be interested in:
http://www.amazon.com/Quiet-Power-Introverts-World-Talking/dp/0307352145
HA! You remembered that I’m the introvert.
Thanks for the suggestion. I’ve thought of digging into some of those kinds of books. It would be nice to have confirmation that I’m not alone in being a tad frazzled by a world that never shuts off, and the constant “noise” we’re surrounded by — people, cars, computers, news tickers — and that it’s not a weakness, just a different kind of wiring.
It’s funny – I’m *mostly* introverted, but when it comes to food and health, people can’t get me to shut up! People at work ask me questions and I get so into it. Some of them who know me better than others just do it to watch me light up. (In a good way.)
that book was recommended to me by a resiliency expert, ordered a copy right before posting this for you. And yea, folks need to realize this is not about being outgoing or not, but about how we gains or dissipate energy.
Amy, great insight! And as a ‘Paleo RD’ I refuse to be ‘lumped’. Being a member of the AND is not required in order to maintain RD credentialing and I am seriously questioning whether or not to fork over the $220 membership fee this year. I propose we take the AND annual conference by storm this October. Let’s turn this ship around or go down trying!!!
Robb,
I am fascinated by the rise and fall of civilizations myself. So interesting. I think you are right that large and static institutions become sclerotic over time – seems inevitable. If Rome had continued unabated we might still be wearing togas and fighting Germans because institutions and regimes want to keep things the *same* not innovate. Any change threatens their position. The innovation that gained them their position is stifled once that position is attained.
This also happened in China who at one point was probably 200 years ahead of Europe but was passed up and then some. They are just now catching back up.
And who’s to say that we are not leaving a “Dark Age” right now. The 20th century was a depressing mix of economic disasters and huge wars. How much was technology retarded because of WWI and II and the subsequent Cold War as resources were piped to the respective military forces?
The internet has blown things wide open as information is free of government and corporate control. Old institutions, like academic journals, which were useful at one time, are being pushed aside. Viva la revolucion! 🙂
It’d be fantastic if we are emerging form instead of entering into a Dark Age.
¡Viva La Paleo! ¡Viva La REvolucion!
Actually World Wars 1, 2 and the Cold War were major *drivers* of technology, not hinderances. The latter two especially because they directly and indirectly led to the space program, which itself alone has been an enormous driver of technological development.
Robb Wolf you are my hero! I like what you said about trying to change the system from the bottom up instead of taking on the powers that be head on. After living the life ourselves for five years now I find myself wanted to help others who are ‘trapped in the matrix’ and have been been looking at what course of study to follow to get a ‘certification’ in nutrition. It seems like every second real food blogger has an IIN qualification these days and at first it gave me pause but now I just think that every one of those is another person with a commmunity that they will lead out of the system. More people eating real food and using food as medicine rather than looking to yet another drug to ‘cure’ what ails them, rather than listening to the ADA or any one of the other misguided and subverted Organizations.
I have doubts sometimes about my ability to help people because there are people like you and Chris Kresser and Diane Sanfilippo who are so exceptional and know so much more about nutrition and the human body … but this weekend my first client broke down in tears because she is rediscovering her body that she “become disconnected from” because there was too much pain and heartache associated with it. Her face lights up when she talks about the fun she is having cooking real food and she shows me the pictures on her iphone. She is planning to go rollerblading sometime after just four weeks ago having to walk down stairs backwards because going down forwards hurt too much. Just by knowing what I do and having an honest desire to help people I can make a small change from the bottom.
Not a small change, a HUGE change.
If only there was a ‘Like’ button! Thanks!
Yeah – I like that “like button” concept as well. I keep looking for it over and over with all these great responses.
You’re the man, Robb.
You are Paleo Baby Jesus! Preach it brother!
HA! Hopefully things end better for me!
The North Carolina Board of Dietetics/Nutrition can be contacted at “[email protected]”
Here is an open letter I just sent…
To the North Carolina Board of Dietetics/Nutrition,
I am writing because I recently foundout about the lawsuit you have brought against Steve Cooksey, threatening to put an injunction against his website (blog), all for promoting his unlicenced opinion. This is a direct violation of his first amendment rights. I do not see how the North Carolina Board of Dietetics has taken it upon themselves to put injunctions up on an website that promotes a certain diet, that was not written by a licensed detitian.
I am sure you would agree, that is completely insane. The only moral thing to do at this point, if you have any respect for the constitution and the first amendment, is to drop this suit, and send Steve an apology.
Oh, and great article Robb. As a lover of obscure sci-fi books, the paleo diet, and a libertarian, I was bound to love this post.
I mean this in the nicest way possible, but Robb, your understanding of history is pretty bargain basement.
Firstly, your characterisation of why civilisations collapse is largely false (and while my panties aren’t quite in a bunch, it’s very clear you’re letting your ideology blind you from historical reality). While an overextended military can be a major factor in societal collapse (and sometimes even the driving one), many, if not most, collapses can be traced to environmental factors (ie. destroying your environment’s carrying capacity). The Rapa Nui of Easter Island, the Maya, the Greenland Norse, and the Anasazi all fell prey to the “creeping change” they were causing in their environments and disappeared (which is why I see such a cruel irony in your not-so-cryptic “Then, seemingly overnight, the perspective changed, no ice age for us! Pull out the water wings. Hmm.” comment.)
One thing you did mention specifically was steam power. Hero of Alexandria did invent the Aeolipile, but he did so as a device to demonstrate how weather worked. It’s perfectly conceivable that someone could have figured out how to use it for steam power, but they didn’t. And not because the Roman Empire collapsed either: the thing was invented well before Rome fell.
The truth is that they just never found much of a use for the thing. The device was invented in Egypt and because they already had a fast artery of transportation (the Nile River), the geographic need to create steam engines to power trains wasn’t there. There also was little to no need for steam engines to power any kind of labour-saving device because cheap labour was plentiful in Egypt, and their Roman masters had slaves. The simple fact is that just because we have the technical ability to do something, doesn’t mean it’s literally feasible to do it.
The reason the term “Dark Ages” isn’t used by modern historians isn’t because it’s not politically correct, it’s because it’s not a remotely accurate descriptor of the time period. The so called “barbarian” cultures that overran the Western Roman Empire weren’t particularly barbaric (the Goths, for instance, were refugees trying to become a part of the Empire) and even when Rome was being sacked by the Vandals, the Eastern Roman Empire (The Byzantines) right next door were thriving, and next door to them a few hundred years later the Arabs were entering a Golden Age.
There seems to be this pervasive cultural narrative that Rome fell, the light of learning was nearly extinguished for a centuries then was re-illuminated in the Renaissance… but that’s patently false. Europeans never lost Greek and Roman learning and the Renaissance was actually a cultural movement rooted in nostalgia for Classical times (giving it far more philosophical kinship with the kind of social-conservatism that longs for the ‘good old days’ of the 1950s than any worldview that promotes progress).
I’d have given you more of a pass if you just used “Dark Ages” in a purely metaphorical sense, but you didn’t. (If we’re going to use it soley metaphorically, I would echo an earlier poster in saying that we’re leaving a dark age.)
History is important. It’s as important as understanding the proper science behind nutrition.
Unfortunately, I think this article largley fails. You can’t really draw parallels between the institutionised nutritional ignorance in our culture and the Early Middle Ages. The parallel simply doesn’t exist in a literal sense. What I got from this was a largely incoherent rant trying to connect your politics, an inaccurate historical narrative, and some *really* interesting stuff about some scientists who grasped ancestral nutrition back in the 1960s. That, I think, could and should’ve been more of the focus. The other pseudo-connections with other stuff just muddies it and distracts from the awesome find.
Guilty as charged on the liberal (Bargain basement) use of history, the Wikipedia links describe as much.
Like I said, I was really just steering this towards an homage to Dr. Shatin, but in my mind I DO see a connection between the rise of totalitarianism and loss of progress. Shatin’s work was accurate 50 years ago, it still is today. Why not broadly adopted? Inertia, an almost immune response typ reaction to new ideas, regardless of data.
Well, in the end, he did end up with a 2000+ year legacy and a world-wide following. So, it you want to “take one for the team”, it might speed up the acceptance of your message a little. I don’t really recommend the whole martyrdom thing though, especially with a little Wolf-cub on the way 😉
Hello A.Stev,
I was just wondering, did you wake up this morning and sprinkle stupid into your foldgers, because I prefer unpasteurized cream.
Every “Civilization” you quoted was not an empire. This is why you never see movies where ancients are running while screaming “Oh my god run! The Eastern Islanders are here! They are going to kill us with slings, and charcoal sharpened wood!”
A bargain basement is where you should shop for real history books, because if you think environmental factors took down the Maya you have more problems than a Mexican whore with herpes. Especially since nobody [this includes you A.Stev nice name by the way tool] knows why they fell. It is a great mystery, perhaps though you can link up with the Scooby Doo detective agency to pull the mask off this mystery since you obviously know the answer and nobody else does.
Keep it civil…
I tell my kids what to eat (both of them are in college and Paleo, thank you very much; mom’s not so crazy after all). Is that nutritional counseling? I hope the food police aren’t coming after me!
great article, Robb! in a period when a lot of “paleo” writers are splintering off, i’m glad to see you not only hang in there, but surpass a lot of what we’ve seen already.
it’s common to see old EFFECTIVE ideas get pushed aside as new technologies get everybody excited about novelties — we see it in more fields than just science/medicine! people love the glitter of newness; me, i believe in “if it ain’t broke, don’t fix it,” but also “if it IS broke, throw it on the trash-heap!”
For 99% of what we are ddealing with we don;t need more info, deeper insights, Just to get folks to try it. Not very sexy, but true.
First, great article! Second, reading this really amps me up for my future. I am just finishing up the first year of my nutrition science undergrad degree and I am interested in conducting research later on in the third and fourth years of my undergraduate studies. However, I am somewhat nervous of how a research proposal based in paleolithic ideologies will be received by a group of whole grain worshiping nutrition advisors. Thankfully for you writing this Robb, I have hope renewed, so thank you for everything you do!
Might get you very out of favor!
Robb,
Here’s my nightmare scenario. In the end, after you, Sisson, the Eades, Loren Cordain, Mat LaLonde, Dr. William Davis, and Chris Kresser present all of the scientific evidence, another George McGovern will step forth to tell you the country cannot wait for all the data to come in before making a decision.
“All this has happened before, and all this will happen again.”
Nice BSG reference! yea, and I’m tackling the sustainability issue in next weeks post. THAT is how they will try to ignore the health implications of paleo/ancestral health.
When you speak about entitled class. I assume you speak of the entitled elite who, through various monetary efforts, ” cloud” the science and through ghastly lobbying efforts convince the unwitting public that a nonpaleo diet is healthy. If you are insulting the working class who don’t have time to research what big agribusiness is dishing out by referring to the 99% as “entitled” then I think you are shooting yourself in the foot. You seem like a smart enough fellow to realize that nutritional information is corporate controlled. And that the corporate entitled elite will play a roll in the destruction of our country. It was hard to tell from your article, you may want to clarify.
I’m honestly confused by the question. We have a corporate/Gov culture focussed on producing and selling crap food. That’s one issue. We have another issue of setting up welfare programs which incentivizes people to do nothing other than collect their “benefits.” That’s a whole OTHER problem.
And I completely agree, there is a wealthy class that has seemingly no compunction driving the country over the edge. The book, The Big Short is quite an eyeopener in this regard.
Yes, you sound a bit confused. I’ve read the book you refered to. It explains how the entitled elite managed to screw up finance. But I’m more interested in your take on how the entitled elite handles nutritional information. I assumed the blog was about the paleo diet. Which saves lives. And healthcare dollars. And allows people to work for their families. But it isn’t clear tome that you understand the connection between large agribusiness and the FDA which is owned by large agribusiness. Large agribusiness has a large stake in the nonpaleo diet. So are “all in” and would you like to correct this? I’m going guess that is what you meant by entitled class. With regards to a political argument on a nutritional blog that is based on science.
Brad-
On my night stand I have 6-8 books on the FDA, AMA, Agribusiness etc, i consider myself a fairly well read student on the subject.
I find myself now remembering something my dad said once back about 1960 (I was a teen ager then). Anyway, out of the blue he said “Wheat causes pain”. That was about 42 years ago. I don’t remember the context of the conversation, but for some reason the words stuck in my head. He still ate wheat and other grains, had joint pains and other ailments. He was metal worker, not medicaly trained at all. Mystery.
My first sci fi book that I later found a copy of and reread was “Earth Abides by George R. Stewart”. Great read.
Ken
Interesting. Really interesting!
I love your articles, even when I may disagree with some parts(bit of a history buff and love of sci-fi). I have noticed a definite line between folks who study bio chem and other sciences such as you and those who take the standard RD certifications. On the whole most RD’s (though a few here are the exception of course) are in the SAD or vegatarian camp and tend to spit out the same stuff about diets, even if I get them to admit certain factors about fat or ketones etc, but moment we discuss food it’s right back to requiring carbs for our brain etc. I had been telling anybody who would listen to me about myown success with paleo, plus can regurgitate some of your book and others as if I was a college grad myself. (seriously looking at college again). I can count 3 rd and one nutritionist I know personally that promote paleo or even a paleo- vegatarian (just whole foods no grains) diet, the rest just repeat the same old stuff, and one has a masters in nutrition ( and teaches and yes told me our brains needs CHO to work properly *facepalm*). I have noticed that a west Texas college seems to be putting out more paleo leaning adults than not. Might be recent, but several kids I’ve known have been to this college that even had a few nutrion classes or such tend to avoid or eat very little grains. … I think we might have a chance!
And by the way it was your book, along with a host of others like Mark Sisson, bloggers galore, friends and more that I credit with saving my husband from certain disability and early death. Just wish we had known so much earlier, but perhaps our children can avoid the similar fate of a short life just because of food.
Good stuff Tamara, do you know the name of the school by chance?
Texas Tech out of Lubbock and West Texas state in Canyon near Amarillo.
Don’t think it’s the program in particular, just my anecdotal notice of some kids (granted just those either student pilots or kids of pilot colleagues) that are coming back armed with information along the lines of paleo. Perhaps a professor or two actually teaching real science or critical thinking at least!
The thing is, RDs *DO* learn all the biochem and physiology. As much as some of us like to bash RDs for the recommendations they’re *legally bound/obligated to give,* their education programs really do get into the science.
The problem comes when they THROW IT ALL OUT THE WINDOW the second they learn it, and when they ignore the very clear-cut metabolic pathways in the human body in favor of political correctness or things that *sounds good on paper* but are ultimately just plain WRONG (low fat, low calorie in order to lose body fat, low saturated fat & cholesterol to reverse heart disease).
Rob makes this very clear in the first chapter of his book (or maybe the intro…don’t remember at the moment). RDs and nutrition students most certainly do learn the biochem. Their failure is in connecting the dots and extrapolating the science to living, breathing human beings.
YES, YES, YES – as an RD I took SEVERAL biochem and nutrition/metabolism bio chem courses along with food chemistry, organic chemistry, medical nutrition therapy, medical physiology, anatomy, research and statistics… In fact VERY little of my college education included USDA guidelines. It’s much deeper than that. Amy is right on in saying that the problem is that many RD’s “throw it all out the window” partly because of their beliefs and partly because of the positions they are required to fill. Working for the school lunch program means following the USDA guidelines or lose funding and there are numerous situations like this.
Here are a couple of posts I did on this subject:
http://robbwolf.com/2011/12/28/higher-education-i-want-to-be-a-paleo-rd-but/
http://robbwolf.com/2012/01/26/8110/
What we are working toward is getting more of these non-paleo supporting RD’s and medical professionals to start ‘connecting the dots’. It’s a long process – but we’re going to get there!
Great thought provoking post, Robb – As usual. I shall have to read the book – I love me a good sci-fi book.
I just wanted to make a little correction – Steve Cooksey isn’t a T1D (LADA as was his first claim…) He is actually a T2IDM – which changes a lot of things.
Now, I have been flamed for this in the past – but I don’t disagree with the NC board’s decision to step in and require Cooksey to tone down his activities.
The thing is compicated, sure – but it boils down to how smart you are in giving your advice. I will stand up for anyone giving GENERAL advice in terms of diabetes. I follow and support your blog, (if even sometimes not 100% with the testimonials…)
The thing is when a person starts offering SPECIFIC, INDIVIDUAL advice and couseling to a diabetic without any credentials, and is charging for it like they are a practising dietician, then it’s not so hard to see where the problem comes from.
Mr. Cooksey knows what works for HIM. That’s it. N=1. He has no concept of endocrinology, the finer points of the complete system. To him, it’s simple – keep those blood sugars down, at all costs.
Offering out advice or specific nutritional counseling is downright dangerous. To look at the report from the dietetic boards on Cooksey’s site – you will see where he is counselling a person to reduce their medications by more exercise and diet. I know it might be a shocker for some, but those medications might be the only thing saving the pancreatic function of a recently diagnosed diabetes patient.
Sure, there is a libertarian slant out there. Let’s get rid of licensing because there are lots of doctors out there that are quacks, right? Who do we trust then? Throwing out the baby with the bath water isn’t the answer in my books.
Robb, I think that someone like Dr. Terry Wahls, or Dr. Cordain are the ones that have it right. Run trials with the context of paleo nutrition and it’s efficacy in management of diseases like diabetes. Test the hypothesis, and let’s get the science behind us so it’s like that rolled up newspaper to the ADA.
Allowing Cooksey (and others) to make bold claims of thier dietary regiments and “practise” is doing the same thing as the ADA – stopping at the hypothesis. Sure, N=1, but that’s not science… that anecdotal evidence.
Jason-I hear ya, I’m just not comfortable sitting on my hands to wait for the trials to run. And i know I’ll lose credibility on this but it’s how I feel: the experts are more dangerous than the free lancers at this point. If “everyone” (or just enough people ran that N=1 experiment, decided to largely eat this way, health care catastrophe is avoided, no “proof” necessary.
Damn straight Robb – I agree 100%. What I don’t agree with is when someone starts charging a person for translating that N=1 to a specific dietary plan. We had enough snake oil salesmen in the previous century.
In fact, if Cooksey had just stated on his site his WOE, and didn’t press the issue by “taking the American Diabetic ASS. to task,” it wouldn’t even be a problem.
Believe it or don’t I know some endocrinologists that applaud Cooksey for his balls, and some even (off the record) agree with him, just not the specific and individual counselling without a licence.
Heck, even my endo snickered at the dietary plan given to me. He mumbled something about them always wanting patients to eat too much. LOL
Truths man. Truths.
Whew. I’m fired up!!! I want to run out and scream at the top of my lungs that we need to wake up. I pass on my paleo knowledge to all who cross my path and will listen, and I truly believe that we, as a culture, are beginning to accept the evidence and demand more local, grass fed, organic, non processed energy. I’m beginning to see the changes in choices in the grocery stores. However, it is still so slow and there is so much damage yet to clean up. I wonder if we still have a margin of time to get it right, or if that opportunity has passed.
I’m starting school in august to pursue an RD. I’m definitely interested on what that is going to be like and if I’ll be alone in my paleo ways. However, I have hope there will be more available for me to study and be credentialed paleo-wise in the future. Looking forward to the SUNY program as well. Thank you Robb for busting your ass for our future.
I think you are getting in at a good time…the tide IS changing.
Actually, I think the Dark Ages was a time of serious “deregulation”. It had the scary stuff of marauding criminals and petty gang rule but there was no governing bureaucracy. Unfortunately,the question may be “Do you want a big oaf or a little toad terrorizing you?”
Top of the list for fall of the Roman, Greek, and all of the dominant civilizations was (is) DEVALUATION of the currency. We are experiencing the same thing today with QE to infinity.
This is YOUR blog so be snarky and let the libertarian leanings out. Keep up the psuedoscience. Great post…
Thanks man!
In a proper sci-fi novel, the one who discovers the truth ends up in jail, at least tomporarily. Be careful, Robb!
Jail is great for Martyrdom!
As someone who had to study paradigm shifts within my subject whilst studying for my degree – I would say that NOT using the scientific method properly and dismissing the evidence that doesn’t fit with your view of the world is actually pretty normal within science. I don’t remember as much as I would like to about the reasons that paradigm shifts happen.
But you are utterly and completely right that we might just disappear yet.
The emergence of quantum mechanics was a blood bath in the physics community. It is unfortunately normal.
Your story reminds me very much of a similar story when we see how the connection between H.pylori infections and peptic ulcers has been established. In the early 1960s John Lykoudis, an obscure greek physician received a patent to treat ulcers with antibiotics, but wasn’t able to publish his findings in JAMA. Unfortunately he died before the famous self experiment by Marshall and Warren in the early 1980s which finally earned them a Nobel Price in medicine. Today not even the Wikipedia article on peptic ulcer mentions Lykoudis anymore.
I believe a similar story exists about the guy who connected folate deficiency and neural tube defects. they ran him out of town, 30 years later discovering he was correct in his findings.
“Bread and Circuses” then and now. I’m really excited about your idea for funding scholarships and studies in Paleo. Have you Paleo movers and shakers been talking about how to get this going? I see a “walk for” almost every weekend in my area, and I cringe to think how the money probably goes to pharma research.
Grassroots efforts can work, as Margaret Mead said: “Never doubt that a small group of thoughtful, committed citizens can change the world; indeed, it’s the only thing that ever has.”
Has anyone actually written a sci-fi set in present day of a neo-Roman Empire that had undergone the Industrial Revolution c.2000years prior, maybe done in a steam punk style?? That book/anime series has the potential to be greater than bacon or worse than bread!!
cool post. Roman empire surviving? wasnt there an old star trek episode about that? (bread and circuses)
what I find intriguing about the fall of the Roman empire is that the EASTERN ROMAN EMPIRE survived for like a 1000 years after. Ive tried to find out why- there are many theories, I need to do more research, but I think it may have to do w their reliance on trade, diplomacy and political maneuverings as opposed to a large war machine. They also had flamethrowers! http://www.youtube.com/watch?v=pVhsduCQyIA
You forgot to mention Robert Heinlein- he shaped many of my libertarianesque views. Read Starship Troopers- the movie is complete bullshit- – awesome political commentaries in the book.
Tunnel in the Sky- the survival tests on alien planets have intersting parallels to I, Caveman.
I actually like the movie!
it’s interesting, in 1491 he describes a similar story with part of the Mayan civilization that is less wealthy, not in as good a position regarding resources and food production, but they ARE on an epic trade route. Whereas the other branches of the civ went into serious decline, this part hung on and thrived. Trade Wins Bitches!
Heinlein was just a badass.
hey man! what’s the name of this movie?! =O
OH! Starship Troopers.
the movie in and of itself is not bad per se, but it is not an accurate translation of the novel. They dont even have the powered armor in the movie!
—
been going over the RW archives, tried out your recommendation for phosphatidylserine- 200mg hs. Wow! improved sleep quality/shrinking stubborn fat deposit. I think this is thru decreasing cortisol? Is it ok to take PS regularly- or should it be cycled on/off? Anyways, the shit really works!
I honestly do not know on the cycling…I just added ti back in and sleep went up, libido…damn good stuff. Have you read The Forever War by Haldeman I believe? Solid, piece of work.
I just started taking some phosphorylated serine (Seriphos) not that long ago. I love this stuff.
yeah, i’ve noticed some ‘stiffness’ in the mornings 🙂
since i got your ear, quick Q. I have really long arms, am reading ‘scrawny to brawny ‘ by Berardi and he recommends on the bench press to come down to 90 degrees (at the elbow). but the bro’s at the gym tell me to be a man and touch the bar to my chest. they say that hits the pecs harder. but berardi’s technique allows me to use more wt and i feel less discomfort on my shoulders. so, bar to chest? couple inches higher? or 90 degrees (which leaves the bar a good 8″ or so above my chest)? thanks
The floor press (90* stop) is staple of really big benchers. Do some fly’s of ring fly’s if the 90 is nto “enough” for your chesticles. Stretch tose mambajambas!! BEnching will make that shizz TIGHT.
Institute of Pectology
http://www.youtube.com/watch?v=Kkm8x6Zp-14
http://www.youtube.com/watch?v=fjSCzC4R6gk
Wow, very impressive Robb, thanks for taking the time. That map in the Shatin link showing the distribution of MS cases was sobering.
As for SF, a favorite site/podcast of mine http://www.sffaudio.com/ reviews SF audio books ans short works (much of it public domain and free). Great for busy schedules.
.
Great post Robb. (I’m also a fantasy/scifi geek, so I love the intro).
As much as I believe the establishment is generally anti-Paleo and anti-low carb (and Steve’s particular case probably had something to do with that), I think the case is indicative of a larger issue. For instance, as some have said, we might not want people practicing unlicensed medicine, but what does that really mean? If your son scrapes his knee, and you clean and bandage it, that’s certainly a medical act that a doctor might perform if you took him to a doctor. What’s more, if I actually wanted someone to perform some sort of surgery on me (all the while completely knowing that they weren’t a licensed doctor), why shouldn’t I be able to pay them to do so? Trying to draw that line is arbitrary at best.
In my opinion, the state should be able to control licensing, mostly to preserve integrity of a profession (and, as we all know, limit competition), and one shouldn’t be able to pretend in any way that they are licensed, but it seems like we could assume that the general public is smart enough to decide if they want to listen to someone who isn’t licensed.
I pretty much agree with that. AND that level fo freedom and self accountability just freaks people out.
My brother (who is working on his PhD in Latin/Classics) mentioned a very apt phrase about history, “History doesn’t repeat itself, but it does rhyme.”
As for the issue of Cooksey, his blog, and the supposed need to police such things, well, they make me wonder about the validity of any such authority. Is it really “safer” to remove one man’s blog from the net? His exposure will arguably affect fewer people than the AND regs do, and let’s be honest, if he gave horrible advice, it would be a self limiting phenomenon. Versus the pap that we actually paid for that flows the KG–er, I meant the AND (or whatever state equivalent that might be).
All of this reminds me of a great C.S. Lewis quote:
“Of all tyrannies, a tyranny sincerely exercised for the good of its victims may be the most oppressive. It would be better to live under robber barons than under omnipotent moral busybodies. The robber baron’s cruelty may sometimes sleep, his cupidity may at some point be satiated; but those who torment us for our own good will torment us without end for they do so with the approval of their own conscience.”
Tom! Made my day, amazing stuff.
That’s amazing that Dr. Shatin had it together so long ago, wow. Why did we not know about this?
This post really got me fired up! This is why I’ve followed your work for these years and why I wanted to be a part of the team and help in any way I could. Let’s make this change happen!
I’ve been trying for a long time to get the people in my life to understand the difference between correlation and causation. It’s nerve wracking and heartbreaking. I can’t tell you how many times a day I want to tear “food” out of people’s hands, and scream and jab my finger at the mile-long ingredients lists and the unpronounceable chemicals and demand to know what part of that sounds like something they should eat. It boggles my mind that a trash rag magazine with a Cabbage Soup diet is trusted and valued more than a methodical, scientific study backed up by actual experimentation… It makes my head hurt.
Right now, I’m finishing my BA with premedical requirements to become a DO. I like the holistic philosophy, and I see more willingness from DOs to look beyond the “done thing” to discover a new way to treat patients. All I can do right now is bide my time and continue being my own n=1 experiment in paleo eating, and hope that through my example and through earning legitimate credentials I can help change the way people think about how they treat themselves. I get my blood panels checked, I track my weight, I take pictures… they’re going to have to admit they’re wrong sometime!
Until then, I’ll keep amassing biochemical and physiological knowledge and eating delicious food while they slowly poison themselves with brown rice and margarine.
Had I gone the DO route I suspect I’d have finished meed school, good for you.
I love everything you wrote here. I’m a Chiropractic student and have been doing a lot of reading in the nutritional field. Why? Because it’s part of my scope of practice in California. I started reading into paleo a while back from Mark Sisson’s work and have read into it much more since then. I currently follow a Paleo diet and since having my girlfriend do it with me, because it’s easier to do something when someone else in a relationship does it with you, she’s been feeling much healthier. Apparently at the time she was constantly feeling sick and out of it, which I wasn’t really aware of, and they went away. She just read a book called Wheat Belly that I think people should read. One part in it that I like is the author talks about the evolution of grains from Einkorn Wheat and how what we have today barely resembles it. He did an experiment on himself trying wheat bread and einkorn bread and monitored how his body reacted. Oh did I mention this guy is a medical doctor (i think he may be a surgeon but can’t remember well enough). http://www.amazon.com/Wheat-Belly-Lose-Weight-Health/dp/1609611543/ref=sr_1_1?ie=UTF8&qid=1335641050&sr=8-1 Check it out, it’s a really good book and offers a slightly different spin on Paleo. I forgot to mention that I’m new here but I will be bookmarking you blog and reading it often.
Daniel! Glad to ahve you here. Yea, Dr. Davis is a good friend, we had him on the podcast when his book first launched.
Thank goodness my Certified Nurtrition Counselor/Personal Fitness Trainer daughter Kari Utz Wolsky clued me in a few years ago about the importance of eating Paleo!!!! Having had Severe RA for 50 yrs. since I was 20, finally I knew how many foods I routinely ate (and thought were good for me) were actually causing my RA symptoms to be MUCH worse!!! Such as 100% Whole Wheat Bread/cereals and LOTS of dairy products!! (Had often asked my RA specialist if what I ate might aggravate my RA and the answer was always “What you eat doesn’t matter.” YIKES!!!) I hadn’t even learned about truly good eating as I trained to be an RN back in the 60s.
So for the past 50 yrs I’ve been on many scary drugs with horrible side effects, had to have many surgeries,( most recently both knees were replaced).as my joints continued to desintegrate and my symptoms continued to worsen slowly but surely (and at this time I was raising 4 kids alone and trying to work 3 jobs 7 days/wk), I kept thinking I wish someone could tell me what food to stay away from above and beyond the “nightshades”…finally I learned from Kari, tried her Paleo suggestion and it was like magic within a few weeks of eating Paleo. My RA symptoms—the pain, stiffness, swelling — started to subside and for over a year and a half I have had minimal discomfort in my joints, sometimes none , plus I am more energetic, more cheerful usually and sooooo thankful!!!
That was a truly fascinating post, Robb!!!
Have you read 50 Degrees Below by Kim Stanley Robinson? It’s a science fiction book and while the politics wouldn’t be right up your alley, it is otherwise very interesting, and the main character is always trying to live a more paleo lifestyle and do things that work well for our paleolithic brains. There’s a kind of running-while-throwing disc golf that is interesting. Parts of the book are slow-moving but the stuff where Frank is trying to figure out a paleo lifetsyle in the city is really neat.
Dr. Shatin was amazing, figuring out all that stuff so long ago. It’s too bad that his ideas didn’t catch on widely. That reminded me of Ignaz Semmelweis, a hero for my profession (midwifery) because he figured out in the first half of the 19th century that doctors needed to wash their hands between patients to prevent spreading childbed fever, which was the major cause of maternal mortality at that time. His ideas were derided at the time because it was considered outrageous to suggest that doctors needed to wash their hands, because “doctors are gentlemen, and gentlemen have clean hands.” He saved many lives where he was able to institute handwashing protocols in certain wards, but fell into despair because his ideas weren’t accepted and women continued to die in other wards and hospitals. He became obsessed with talking about handwashing and eventually was hospitalized and considered insane, and it wasn’t until decades later that medicine accepted the importance of handwashing.
Paleo cured my cancer.
Thanks to Bill Perkins for cleaning up the PDF files to make them more easily readable
Great stuff on Shatin. I might also recommend Richard Mackarness as someone who promoted similar ideas (in Psychiatry mostly) and may have been aware of Shatin’s work.
He wrote a book called “Eat Fat and Grow Slim” in 1959 and later promoted a “cave man” diet and grain avoidance in “Not all in the Mind” 1975.
As for politics, have you read Oswald Spengler, “The Decline of the West” or later works? He was probably the first to point out the factors that eventually doom all cultures that form civilisations. He correctly predicted the duration of Hitler’s Reich. He also said “Optimism is cowardice”. Yikes.
Awesome piece Rob! I also understand that taking a political stance can be harmful to a financial venture such as this so I applaud your efforts. I find it frustrating that in so many areas we have to end up relearning what we already know. I am hopeful that the internet will be a game changer when it comes to that but in my mind I think it could still go either way. Keep it up!
Dear Rob,
I have been trying to get a hold on the papers on dktr R. Shatin but I cannot find them anywhere and it drives me crazy. Would it be possible for you to send them to me?
I would appreciate it immensely! Mieke
Did you mean the ones linked in the post
http://robbwolf.com/wp-content/uploads/2012/04/Shatin-Paleo-Diet-19641.pdf
http://robbwolf.com/wp-content/uploads/2012/04/Shatin-Paleo-Diet-19671.pdf
or were you looking for something else?